镜片设计的基础

作者：GREGORY L. STEPHENS and JOHN K. DAVIS      

译者： Lisa Huang                                                            

原文出处：http://www.eyecalcs.com/DWAN/pages/v1/v1c051b.html#ato

视远点球面

当远距离的图像通过矫正镜片成像在患者的视远点时，患者的屈光不正就被矫正了。当患者转动眼球通过镜片不同位置观看时，视远点也会跟着移动，移动的轨迹会形成一个平面，这个面就叫做视远点球面。镜片设计的目的就是使离轴的物象能落到视远点球面上，而离轴像差必须达到最小才能实现这个目的。

镜片像差（视野偏差）

七个常见的镜片像差现象中^[11]，有四个会极大地降低通过镜片非中心区域观看的视线，即径向像散或斜轴像散，像面弯曲（度数偏差），畸变和横向色差。这些像差现象会降低可用视野，也叫做视野偏差。镜片的放大效果以及两个镜片之间放大效果的差异也是设计中要考虑到的因素。镜片设计的目的也可认为是使透过镜片后的可用视野最大化。虽然另外三个像差现象——球面像差，斜射球面像差和纵向色差——在其他类型镜片的设计中比较重要，但对眼镜片的视觉影响很小。

当患者观看一个点状物体且该物体不落在眼镜片的光轴上时，它透过镜片形成的像就不再是点状的了，而也许是两条相互垂直的线（线焦点），其中一条较靠近镜片（图3）。这就是径向像差或斜轴像差。径向像差对成像的影响基本上类似于斜轴像差。如果像的其中一条线落在视远点球面上，患者看到的就是一条线。如果两条线焦点跨越在视远点球面的上方，就不会形成清晰的像，而是一个模糊的圆形。在其他相对位置上，所成的像都是模糊的椭圆。这两条由于径向像散产生的线焦点之间的距离被称作斯图姆间距，而在它们之间形成的失焦的圆形像被称为最小模糊圈。^[12]

图3为一束光线透过眼镜片后在离轴点的径向像散。由于光线必须通过瞳孔，透过镜片的光束便受到了尺寸的限制。左图中放大的插图显示了斯图姆间距的部分，和它的两条线焦点（其中一条较靠近镜片），以及最小模糊圈。

如果通过有径向像散的镜片查看一个较大的离轴物体，那么物体上的每个点都会成像为离镜片不同距离的两条线焦点。在图4所示例子中，十字目标物的垂线在离镜片较近的焦点处成像为许多条短的水平线。十字的水平线也同样成像为许多条水平线，但这些像沿着线的长度交叠在了一起。如果这个像正好在患者眼睛的视远点球面，则他看到的十字的水平线便会非常清晰，而垂直线就会比较模糊。在离镜片较远的焦点处，情况便会相反，即看到的垂直线非常清晰，而水平线是失焦的。在最小模糊圈里，十字上所有点的像都是失焦的圆圈，同时水平线和垂直线的像会有等同程度的模糊。在离镜片不同距离所成的像都是不同的。

图4. 当通过有径向像散的镜片观察一个较大的物体时，在斯图姆间距方向上的不同位置所看到的像都会不同。

    

形容径向像散形成的线焦点有专门的术语。假设患者从横向的角度透过镜片中心察看一个十字。如果把患者的视野想象为垂直平面上的一个圈，十字就会在这个圈的横向边缘上，并且十字的垂直线会与这个圈相切。这条垂直线通过镜片形成的焦点称为正切焦点，而该焦点位置相对于视远点球面的误差称为切向误差。影响到水平线的焦点误差被称为弧失误差，而这些线的焦点被称为弧失焦点。如果患者要往上看位于视野顶部的十字，十字的水平线是与视野圈相切的，它的焦点即为正切焦点，而垂直线成像后会形成弧失焦点。正切焦点与弧失焦点的误差会随着其与镜片中心距离的增加而增加。

径向像散镜片形成的两条线焦点也许会在视远点球面的前面或后面，或横跨整个视远点球面。视远点球面的屈光度为零，与其相对的两焦点位置处的屈光度平均值被称为光度误差。光度误差会随着与镜片光轴距离的增加而增加，因而较大物体的像表面是弯曲的，便形成了象场弯曲（图5）。一般来说，光度误差与径向像散不能同时避免。^[13] 当没有径向像散时，光度误差残值仍会存在；当没有光度误差时，径向像散仍会存在（图六）。与其尝试直接矫正光度误差，镜片设计者不如尝试最小化弧失焦点或正切焦点的误差。弧失焦点或正切焦点的位置在视远点球面后方（负误差）比在其前方（正误差）对视敏度影响更小，因为患者可以在适应的过程中自动把负焦点往前拉到视网膜上。因此，完美平衡弧失误差和正切误差，即在视远点球面一前一后，并不一定会达到离轴成像的最佳效果。最好的办法也许是允许更大的负误差去矫正正误差。

图5.当径向像散被矫正后，扁平物体的像会弯曲。这个像曲面弯度就被称为像场弯曲。像位置与视远点球面在指定离轴位置之间的屈光差为光度误差。

图6.  A. 当径向像散被矫正后，两条线焦点重叠形成一个点物体的点像，但这个点像不在视远点球面上，从而造成了光度误差。B. 当正切焦点和弧失焦点与视远点球面等距时，不存在光度误差，但存在径向像散。（Atchison DA: The clinical importance of spectacle lens base curves. Clin Exp Optom 69:31, 1986修改而得）

径向像散和光度误差两种像差中，究竟矫正哪个更为重要？这个问题多年来在眼镜业一直存在持续的讨论与争议^[14]。最近的镜片设计为了中和这两者，正在尝试最小化两个像差但同时不完全矫正其中的任何一个。这个话题我们会在镜片设计的演变一部分中进行更具体地探讨。

横向色差是由于色散造成的，即折射率在不同眼镜片材料上由于波长不同产生的变化（图7A）。当患者透过镜片横向地观察一个点状物体时，物体所反射出来光的波长是不同的，因此这些光的折射也会不同，会把像“涂抹”出它的组成色（见图7B）。如果该物体不是点状的，而是个向外延伸的物体，例如一个十字，色散的效果便会不同。十字垂线所发出光的每个波长也会有不同的折射，使得垂线像的周围会有一圈颜色。但是，十字水平线的像相对来说不会受到影响，因为色散会沿着水平线形成它的组成色，因而除了两头以外无法被注意到。因此，我们可以说横向色差的影响也许对于正切焦点更为重要，而对弧失焦点较小。横向色差的效果类似于透过棱镜所看到的色散效果。

图7. A. 色散是折射率随着波长变化而发生的变化。色散在所有镜片材料中都会有，且同时会造成色差。 B. 当一束白光从镜片的边缘透过时，其中不同的波长就会发生不同程度的折射，形成横向色差。

镜片的棱镜效应随着镜片度数的变化而变化，也随着光穿过镜片时与光学中心距离的变化而变化。它们之间的关系被称为普伦蒂斯法则^[15]：

P = h × D

（1）

其中P代表棱镜屈光度，h代表光线离镜片光学中心的距离，以厘米为单位，而D则代表镜片的屈光度。镜片屈光度越高或视角越大，棱镜效果越明显，因此与棱镜效果相关的横向色差在同样的情况下也会越厉害。高折射率的玻璃片和高折射率的塑料片材料，比冕牌玻璃和CR-39塑料色散更严重，且横向色差的问题对这些材质的镜片也更为重要。临床上，患者透过这些高屈光度，高折射率的镜片观看时，只有当其不通过镜片中心观看时才会反馈视物周围有彩色边纹，但当镜片屈光度低于5.00D左右时，患者很少会说有彩色边纹。镜片设计师无法改变给定材料的色散效果，所以从某种意义上说，我们对横向色差一点办法也没有。然而，恰当的镜片设计可以最小化或去除其他的像差，眼镜诊疗室里恰当的装配技术也可以最小化整个离轴的模糊度，同时改善视敏度。

畸变是由于从镜片中心到边缘的放大程度不同而产生的像差（图8）。它对成像的分辨度几乎没有影响，但会影响到像的形状。近视度数很高的镜片，放大程度会沿着中心到边缘递减，当一个较大的物体透过这样的镜片成像时，相比较物体离镜片中心较远的部分，较近的部分会被更多的放大，从而形成了“桶形”的像的畸变。远视度数很高的镜片，放大程度会沿着中心到边缘递增，从而形成“针垫形”的畸变。而畸变的效果在近视度数高（无晶体）的镜片上更为明显。佩戴这类镜片的患者通常会反馈说，从离轴位置看门框和其他长方形或正方形的物体时会出现弯曲的现象。另外，当患者戴着厚的远视镜片转动头部时，由于放大和畸变同时存在，会有正在游泳的感觉。这个问题可以通过较平的非球面设计得到大大的改善。

图8. 畸变会影响像的形状。A.“桶形”的畸变。B.“针垫形”的畸变。

简单的演示

如果一个人拿放大镜看一本印有垂直线和水平线的杂志或一张图纸，就会观察到镜片的像差效果。当放大镜正对着纸张且与视线垂直时，视野的效果从中心到镜片边缘都会不错。如果放大镜的顶部稍稍往上翘起，透过顶部看下去，水平线会变得模糊，有色差和弯曲，而垂直线会在比较聚焦的位置，不弯曲且没有变色。如果放大镜的其中一边稍稍翘起，类似的现象也会发生。模糊来源于正切误差，色差来源于横向色差，而弯曲来源于畸变。水平线与垂直线模糊的不同程度是由于离轴或径向像散。

折中的需要

从最简单的层面来讲，镜片的设计过程会涉及到计算镜片前后弯度在每条径线上的弧失误差与正切误差。这个计算用来决定哪一种组合可以达到最好的离轴光学效果。表面弯度的变化会产生不同的像差组合。有些误差会一直存在，即使换成非球面也依旧存在。

因此，镜片设计过程是一个折中的过程，从各种方案中选取最优选项。60多年来，哪一种方案是最优的在专业领域和广告领域都一直备受争议。争议仍然存在的原因之一是患者很少有机会比较两个设计。另一个原因则是测量离轴像差的仪器很少见。最后，关于各种镜片设计的实际信息十分欠缺。生产商可以提供更多的信息，但是“完整的”信息处理起来很难。要描述现有的各类型和各种设计镜片的性能需要好几百张表格的数据。但是，我们会试着解释镜片产品之间的区别，以及这些区别的大小程度。

 

镜片设计的几何基础

图9显示了镜片与眼睛之间理想的几何关系。图中，镜片的光轴用一根假想的线来表示，它连接了镜片两面的曲率中心，又同时通过镜片的光学中心。设计镜片时，我们都假设光轴会通过眼睛转动的中心。在镜片设计中，眼睛转动中心被称为整个系统的光阑，因为它的位置决定了哪些光线会到达离轴观看时的中央凹。光阑距离，或转动中心的距离，即为镜片背面到转动中心的距离。传统上说，这个值可以假设为一个常数，一般为27毫米^[14]，但如果就这个值的整体分布来说，它的变动也很大。镜片设计者会根据这个值来计算镜片的最优基弯。转动中心距离是顶部距离与瞄准中心距离之和，即角膜顶部到转动中心的距离。

图9.为框架眼镜的示意图。OC为光学中心，OA为光轴，而光轴应通过眼球转动中心（CR）。为了计算镜片像差，光束一直延伸到视远点球面（FPS）。误差在这里指的是参考球面（RS）。光阑距离，或转动中心距离，即为瞄准中心距离（SCD）与顶部距离（V）之和。

让我们假设镜片配戴时的顶部距离是与屈光检查中的一致的，或处方中已经对两者间的差别做了补偿。一个远距物体的像因而会落在视远点上。当眼球转动而从离轴的位置观看时，视远点也会随着转动，转动的轨迹形成了视远点球面。注意光线是通过眼球转动中心的。按照惯例，离轴物体发射出来的光的焦点屈光位置是根据参考球面而计算的，这个参考球面与镜片背面在光学中心相切，并以眼球转动中心为中心。成像的误差因此可以表达为在视远点球面上与焦点期望位置的屈光差。

 

直到最近，在眼镜片的整个发展史中，连接患者与镜片的基础输入一直是转动中心距离。这个镜片-眼睛系统里的光阑正是所有视线的相交之处。

典型的佩戴几何

图10解释了镜架和镜片在脸上的位置。大部分镜片佩戴时底部会向眼睛稍稍偏一点，这个偏角的大小约为10度，叫做倾斜角。同样，大部分镜架，尤其是塑料镜架，会设计成佩戴者往前看时，镜片中心比瞳孔低几毫米。幸运的是，这两种情况的结合可以保持眼球转动中心往镜片光轴靠近（在3毫米以内），且镜片顶部会几乎自动落在参考球面上。简而言之，图10为图9往下倾斜的示意图，并加上了一些可变性。

图10为一个典型的镜片佩戴情况。大部分镜片佩戴时镜架底部都会微微向脸部靠拢（倾斜角）。镜片的光学中心应低于往正前方看时的视线，这样镜片的光轴才会通过眼球转动的中心。（Davis JK: Prescribing for visibility. Probl Optom 2:131, 1990修改而来）

评估一副镜架是否配戴到位，可以通过想象一条在eyewire竖直点与其垂直的线，并向眼球延伸如图10 所示。如果用一把尺靠着镜架和脸颊测量，尺的边缘可以帮助我们看到这条线。这条线指明了镜片光轴的位置，且它看上去几乎穿过了转动中心。这个点如图所示，位于眼角的后面。

因为眼镜片最大的用处是用来看正前方和下方，因此正常的倾斜角不仅外表好看，在功能上也符合人意。大部分处方虽与图10中所显示的理想状态稍有出入，但不会造成很严重的误差。然而，配戴晶状镜片和高度数近视或远视镜片时，装配员必须十分小心才能使倾斜角与镜片中心的竖直高度达到合适的位置，让光轴尽量穿过转动中心。惯例上，当患者的视线与太阳穴平行时，每2度的倾斜角，光学中心需相应的比瞳孔中心低1毫米（对于正常的6-10度的倾斜角，需比瞳孔低3-5毫米）。这个规则对于高度数和非球面镜片也十分重要。

镜片设计中也可以考虑眼球位置在竖直方向的变化，但到现在，还没有人考虑到这个。有时仅仅为了说明，会计算并公布某些所选镜片设计中竖直偏离所产生的影响^[16][17]。镜片，角膜和转动中心之间的纵向或轴线关系也不易调整，一直以来，这些数值都是主要的输入变量，用来决定镜片的设计。

视角

大部分镜片为了最小化视野误差，把光学中心每边与光轴的角度设计成30度^[14]。有些度数很低的处方甚至会使用40度。这些数值一直被批评太大，因为大部分患者不会将眼球转动到离光轴30-40度的地方。然而，虽然大部分患者不会这么转动眼睛，但镜片的正前方位置或零点不一定就是光学中心。习惯性姿势中，这个位置通常都在光学中心上方，且在光学中心两边以外。这个非中心的起始点结合眼球各个方向的微小移动后，视角度数便会增大。

当设计聚碳酸酯镜片系列时，Davis重新分析了视角问题^[18]，如图11所示。他指出，对于典型的眼镜配戴者来说，正前方的位置大约在光学中心上方约5毫米处。在这个零点周围有一块患者可以不用移动头部就看见的视野范围。不同的患者可以有不同的零点，但都会围绕在这个零点周围，从而形成一组零点位置（图11显示了一圈围绕这个中心的点）。然后，Davis假设对于每个零点位置，都有一块配戴者不用转动头部就看见的椭圆形范围（竖直20度，水平30度）。这样就形成了一组椭圆形，而在椭圆形范围内的视野误差都应被矫正。

图11.不同的配戴者透过镜片看到的椭圆范围都有不同的中心零点。这些椭圆的外缘所对的角与光轴之间大约为28度（Davis JK: Prescribing for visibility. Probl Optom 2:131, 1990修改而得）

这些椭圆所对应观看者的鼻子边缘和太阳穴边缘与光学中心的角度为25-30度。Davis选择了28度作为他设计镜片的标准。要注意的是，虽然眼球水平转动只有15度，但矫正视野误差所需要的视角要远远大于它。然而，一个28度的视角所代表的只是镜片上一个直径为28毫米的圆。

镜片误差的数例

假设之前镜片几何部分提到的信息都是给定的，根据准确的面到面光线跟踪法，就能计算出弧失焦点误差值和正切焦点误差值^[14][19]。表1为一块-3.00D的冕牌玻璃镜片在不同转动中心距离和不同前弧线（基弯）时所计算出的误差值。选择与每个基弯相对应的后弧线（眼弯）时，要选择可以给该-3.00D镜片提供适合度数的，同时也要考虑到该镜片2mm的中心厚度和1.532的折射率为。

 

表1. 球面镜处方3.00在30度时的视野误差*

	CR距离, 24 mm			CR距离, 27 mm			CR距离, 30 mm			CR距离, 33 mm
前弧线	顶端距离, 10 mm			顶端距离, 13 mm			顶端距离, 16 mm			顶端距离, 19 mm
后弧线	T	S	A	T	S	A	T	S	A	T	S	A
+ 7.00	0.10	0.11	0.01	0.18	0.14	0.04	0.24	0.16	0.08	0.30	0.17	0.12
10.00
+ 6.00	0.02	0.09	0.07	0.11	0.12	0.01	0.18	0.14	0.04	0.24	0.16	0.09
9.00
+ 5.00	0.07	0.06	0.13	0.02	0.09	0.07	0.10	0.11	0.01	0.17	0.13	0.03
8.00
+ 4.00	0.18	0.03	0.21	0.09	0.06	0.15	0.01	0.08	0.09	0.06	0.10	0.04
7.00
+ 3.00	0.32	0.01	0.31	0.23	0.01	0.24	0.15	0.04	0.19	0.08	0.06	0.14
6.00
+ 2.00	0.48	0.06	0.42	0.40	0.04	0.36	0.32	0.01	0.31	0.25	0.00	0.25
5.00

T, 正切; S, 弧失; A, 散光. CR, 转动中心.
*在无穷远（20英尺或以上）距离的物体。顶端距离仅为估计值。

假设患者在转动中心距离27mm的位置戴着这块-3.00-D的镜片，基弯为+3.00D。当患者沿着与光轴30度角的方向往上看时，正切误差为-0.23D。弧失误差为+0.01D，本质上可认为是零。散光误差，即两条线焦点的差，为0.24D。患者从这个位置（大约镜片中心上方16mm处）透过镜片看，所得到的处方不会是-3.00D，而是-2.99 -0.24 × 180 （或 -3.23 + 0.24 × 090）。如果从侧面看同样的位置，散光轴则会偏移90度。

这个例子中的度数误差，即弧失焦点与正切焦点的平均值，为-0.115D。其中一个焦点正好在视远点球面前面（0.01D），而另一个几乎在球面后面0.25D的位置。因此，当患者从离轴方向看时，屈光不正会被过度矫正或度数过深。如果患者稍稍调适一下，焦点会往前拉到视远点球面以外，同时度数误差也会消失。

如果镜片前表面的基弯为+6.00-D，散光会变为-0.01D，本质上可认为是0，但在镜片周围距离中心30度（16mm）的位置度数误差会达到+0.115D（大约1/8D）。这两个例子中的数值看上去不大，但就折射精确度与镜片制造而言还是非常大的。

镜片设计中另一个较为复杂的方面是大部分镜片为球柱镜。每条主子午线都有自己的一组需要矫正的弧失和正切误差。之后我们会更详细地讨论球柱镜镜片设计。

镜片设计的演变

Davis^[14]和Atchison^[20]详细地回顾了眼镜片设计的历史发展。这部分中的很多信息都基于他们的研究。 

 

矫正曲线或最优曲线镜片，即特别为避免离轴像差所设计的镜片，最早可以追溯到1804年的沃拉斯顿。但现代商业镜片设计最早开始于1911年的美国，当时蔡司的Von Rohr获得了Punktal镜片的专利。这是一种“点焦”镜片设计，它的目的是为了完全矫正倾斜视线下的径向像散。从表1的数据来看，假设转动中心距离为27毫米，Von Rohr本可以为这块-3.00-D的镜片选择约为+6.00D的基弯。Von Rohr设计中存在的一个问题就是，为保持点焦矫正准确，每个镜片度数对基弯的要求都会不同，使镜片生产又困难又昂贵。

1917年，美国光学仪器公司（American Optical Company）的物理学家Tillyer，申请了另一种不同的镜片设计专利，这项设计可以允许同时存在径向像散和光度误差。设计镜片的过程中，Tillyer相信他应以镜片市场上的订购与库存流程作为自己的向导。他发现，当患者度数较低时，处方至多按照0.12D的间隔来定。对于度数高的，也许会结合球面度数与散光度数按0.25D的间隔来定。他认为，如果患者的实际处方承受度不接近0.25D，那么就没有必要矫正斜轴像散到屈光度的百分位。因此他将径向像散的承受度允许到最大，等同于当时习惯性使用的处方精确度0.12D。

Tillyer的方法使基弯的选择变得更灵活，从而光度误差也能得到矫正。他的理论得到应用后便出现了实用的单光镜片系列。这种设计所挑选的基弯可以同时矫正散光和读数误差，并且比处方里用到的间隔更为精确。

再次参考表1，在转动中心距离27mm位置的-3.00-D镜片，基弯为+5.00D正好满足了Tillyer的标准。当然，我们不能否认0.07D的散光会造成很大的影响。另外，即使+6.00-D基弯可以获得更好的散光矫正，0.055D的平均光度误差（正切与弧失误差的平均值）也只有6.00-D基弯值的一半。+6.00-D的设计是可以接受的，而+4.00-D的设计也几乎在允许范围内（0.15D的散光有一点过多）。任何在这个范围内的基弯都可以满足所需要的矫正。这个例子体现了镜片设计过程中的折中。

还有另一个方法可以说明Tillyer的概念，即一定范围内的镜片度数可以用同一个基弯，又可以同时在允许范围内仍做到镜片像差的矫正。表2对这个特点做出了说明。这里，当球面镜度数从平面变到-5.00D的过程中，基弯一直保持在+5.00D。从平面到-3.00D，散光和度数误差一直保持在0.12D以下，因此同样的基弯可适用于这个范围内任何度数的球面镜片。这种灵活性使得镜片生产商为光学实验室提供半成品毛坯时，只需提供一定数量的基弯。实验室可以根据每种基弯的预定量范围来改变处方。

 

表2.球面镜处方(前弧线+5.00)的视野误差*

		球面镜度数
距离	误差	0.00	-1.00	-2.00	-3.00	-4.00	-5.00
CR距离, 27 mm	T	0.03	0.06	0.04	0.02	0.12	0.24
顶端距离, 13 mm	S	0.01	0.01	0.04	0.09	0.14	0.20
	A	0.02	0.07	0.08	0.07	0.02	0.04

T，正切；S，弧失；A，散光。CR，转动中心。

*在无穷远（20英尺或以上）的物体。顶端距离仅为估计值。

 

现在几乎所有人都用到了这一理念，即镜片度数在一定范围内可用同一基弯，整个处方范围内可用一系列基弯。这个系统减少了镜片的库存，同时避免了每个可能的处方都要准备不同的基弯。当地的光学实验室都存有各个前弧线的半成品毛坯。表格或计算机程序可以告诉实验室工作人员对每份处方应使用哪种毛坯。生产商也会根据类似的这种固定间隔的基弯系统来提供未切割的成品镜片。未切割的成品镜片和半成品毛坯应可以互相匹配。

1927年，博士伦的Rayton把点焦镜片引入了美国的镜片市场，同时将其修改为这种固定间隔的基弯系统。该镜片系列最终成为了著名的正交镜片系列（Orthogon lens series）。有一段时间，大部分商业镜片系列都按照正交镜片或Tillyer的理念来设计，于是人们一直争论那一种系统更好。两个系列在许多处方中的表现是差不多的。如果通过允许部分径向像散来矫正光度误差，或通过允许部分光度误差来矫正径向像散，得到的基弯选择都是一样的。患者的反馈很少会与镜片的选择相关，可能因为患者没有机会将它们进行对比。

Masterpiece系列

镜片配戴时的转动中心距离短的时候可到24mm，长的时候可达33mm。二十世纪六十年代初期，Davis和他的合伙人在设计美国光学公司的Tillyer Masterpiece镜片时，将这个距离可变性考虑了进去^[21]-[24]。只有在转动中心距离27mm到33mm的范围内都表现良好的基弯才会被选中。他们将最初的Tillyer设计原理修改为优先考虑正切误差，因为他们认为正切图像的细节不仅会被焦点误差弄糟，也会受到离轴观看时棱镜效应所产生的横向色差的影响。表1中，+4.00D基弯（+3.75D是被选基弯）所对应的正切误差几乎为零。看远处时强调矫正光度误差，看近处时强调矫正径向像散，这样，镜片的表现不管是看远看近都能得到保持。这些镜片的基弯要比最初的Tillyer镜片系列更平一些。

1971年，为了可以在转动中心距离非常小的情况下进行矫正，Masterpiece镜片系列进一步修改而为Masterpiece II 系列。径向像散、弧失误差和正切误差的允许范围被修改到可以矫正正值误差和正值散射，但同时要牺牲对负值误差的矫正。一块-3.00-D镜片所选的基弯为+4.25D。表1中显示，镜片在所有配戴距离处都可以保持合理的表现。Masterpiece II 系列的基弯比最初的系列要更陡一些。

Masterpiece镜片系列由于是第一批度数为负的柱镜镜片而显得格外特殊。这种设计的复曲面放在了镜片的背面。与正值柱镜相比，负值柱镜设计有许多优点，下一节中会具体阐述。Masterpiece镜片一开始流行，其他生产商就开始逐步引入负值柱镜设计，玻璃和塑料的都有。现在的眼镜片市场，几乎所有的镜片都是负值柱镜。

球柱镜片的特殊问题

球柱镜片或复曲面镜片存在一个特殊的问题，它只能选择一种弯度来控制两条主子午线的误差。柱镜的度数可以在镜片的任意一面铣磨出来，但由于很多原因，几乎所有现在生产的镜片都是负柱镜设计。首先，负柱镜设计中，矫正离轴像散更为重要。虽然有必要折中两条主子午线的矫正，但这样的折中一般来说在负柱镜中的效果比正柱镜中更好。实际上，正柱镜在度数为正的处方上略有优势。其次，负柱镜设计中，主子午线之间的放大效果差别会减小，镜片的子午线放大效果差别也会减小。第三，几乎所有现在的多焦点镜片都是负柱镜设计。当患者的眼睛开始老花，如果他已经戴了负柱镜镜片且放大效果不变，那要适应双焦镜片对他来说就没有什么问题了。最后，负柱镜外表也更吸引人。大的柱镜放在镜片前部时会很明显，但负柱镜就可以隐藏镜架后面柱镜产生的边缘厚度变化。

 

图12说明了球柱镜片存在的设计问题。CR-39塑料镜片是一种度数为+4.00-2.00（或用正柱镜表示为+2.00+2.00）的负柱镜。给定一个基弯，镜片的两条主子午线有各自不同的正切和弧失焦点。这张图显示了，视角为28度时，对于不同的基弯，这些误差是如何在这两个点影响到镜片处方的。例如，点A处，+7.25-D的基弯在处方中的球面误差为+0.25D，柱镜误差为-0.45D。患者通过点A观看也就是通过度数为+4.25-2.24的镜片观看，柱镜轴取决于镜片在镜架中的倾斜情况。

图12为+4.00-2.00的CR-39塑料镜片在平均配戴距离上，对于不同基弯所对应的各种镜片内部误差。与光轴成28度的两点决定了球面误差和柱镜误差。点A在柱镜轴子午线上，点B在柱镜光度子午线上。模糊度为四个误差中最大值的绝对值，其中球面误差为负时要乘以0.5个径向像散，然后再加上光度误差。（Davis JK: Prescribing for visibility. Probl Optom 2:131, 1990修改而来）

由于两条主子午线的四个误差会变化，要决定单个最优的基弯非常复杂。为了达到这个目的，镜片设计师经常对每个基弯使用单个数值，即“模糊值”，来评估设计的质量。正如之前提到的，在折射误差对视敏度影响的基础上，模糊值将离轴镜片像差与像差对视敏度的影响联系在了一起。这个例子中，模糊值被定义为每个基弯的四个误差中最大值的绝对值，如果是负球面误差则当做散光误差的一半，如果是正球面误差则等同于散光误差^[6]。由于患者可以自我适应来最小化负度数误差的视觉效果，负度数误差与其他误差相比占的比重最小。模糊值在基弯大约为+9.25D时最小，也就是说+9.25D是这个镜片度数的最优基弯。

图12分析了镜片设计时所有重要的球面和柱镜度数组合。它体现了设计过程的复杂性。这个计算曾经是用手算的。计算机的引入加快了设计的过程，同时也带来了更复杂的设计，例如非球面镜片。

放大效果与镜片设计

镜片的放大效果

眼镜片的放大效果和离轴像散应受到一样的重视。患者戴上新眼镜时若折射度适合，会有较好的视敏度，但会反映说看到的地面不平，或楼梯的位置不对，或有些东西“看上去就是不对劲”。这些问题都源于眼镜片的放大特性。如果一副眼镜的两片镜片不同，他们所成像的大小也许也会不同。

假设一位患者拿到的眼镜右眼度数为-0.50D，左眼为-1.00D。看的最远的物体的像离右眼距离2米（大约6英尺），离左眼距离略大于1米（3英尺）。所有物体看上去不仅感觉更近了，也更小了，而且两眼看到物体的大小也有可能不一样。患者通过眼镜看到的物体距离和大小与其不戴眼镜时看到的相矛盾。由于两个视网膜像尺寸的不同，产生了空间和立体视觉上的双筒望远镜效果，物体当然会看上去不太对劲。

 

值得注意的是，大部分患者都可以快速地适应这个情况。这组新的光学输入与其他的感官输入相关，于是患者可以开始在更好的视敏度下继续工作。大部分人都很容易就适应他们的第一副眼镜或处方上的变化。但是，他们的适应能力会因为他们的适应意愿不同而改变。一些患者会保留他们的旧眼镜，然后与新眼镜替换使用，即便两副眼睛的处方相差很大。另一些患者一旦看到像有大于1毫米的误差便会马上要换眼镜。

量化放大效果

眼镜片对视网膜像大小的影响（镜片放大效果）可以根据以下公式^[25]计算：

（2）

SpectacleÜqnMagnification = Üp311 - (tn) D₁ Üp8 × (11 - hD)

 

其中t为镜片中心的厚度，以米为单位，D₁为真是前弧线（不是1.53）屈光度，n为其折射率，h为镜片背面到瞳孔进入点的距离（顶端距离+3mm），以米为单位，而D为镜片背面顶端的屈光度。等式的第一部分包含了镜片的厚度和前弧线，称为形状系数，第二部分被称为光度系数。形状系数总是可以告诉我们镜片的放大效果，而光度系数则告诉我们正屈光度镜片的放大效果和负屈光度镜片的缩小效果。

镜片设计师的职责之一就是，当双眼度数不一样时（屈光参差），最小化两眼间放大效果的差异，通常会使用相邻处方间较小的基弯间隔来达到这个目的。工厂生产的未切割成品镜片中，基弯间隔很少会大到1.50D，最常见的都是小于1.00D。半成品镜片中，基弯间隔会大些，但是在更好的镜片系列中，不会超过1.50D。设计不良的半成品系列基弯步会达到2.00-D。如表3所示，大于+5.00D的正屈光度处方，基弯间隔的放大效果差异在临床上已经算非常大了。表3所用的前弧线和中心厚度都是根据聚碳酸酯半成品镜片表中的每个镜片度数来选择的，然后通过之前提到的公式，来计算每个镜片度数的形状和度数放大效果。对于两个度数差在1.50-D或更小的镜片，它们之间的放大效果差异可以达到大约1.5%，但大部分只有1.0%，有些则更少。对于度数小于+3.00D的镜片，它们之间的厚度差异对放大效果差异的影响可以忽略不计。因此放大效果问题的解决方法之一是将两片镜片的厚度订制成相同的。这样，即使是视野矫正较好的不同基弯，不同度数镜片之间的放大效果差异会也会被减弱。

表3 . 所选镜片度数的形状和光度放大值*

镜片度数 (D)	1.53 基弯 (D)	中心厚度 (mm)	形状放大 (%)	光度放大 (%)
+ 6.00	+ 10.89	7.1	5.70	11.36
+ 5.75	+ 10.89	6.0	5.61	10.83
+ 5.50	+ 9.75	6.6	4.70	10.31
+ 4.50	+ 9.75	5.8	4.10	8.28
+ 3.75	+ 8.55	5.1	3.14	6.81
+ 3.25	+ 8.55	4.7	2.88	5.85
+ 3.00	+ 7.52	4.5	2.42	5.37
+ 2.00	+ 6.46	3.6	1.65	3.52

*基弯和中心厚度来源于聚碳酸酯半成品镜片面表。光度放大是由14mm的顶端距离计算而来的。

双眼之间的放大率差异通常来说比较小，一般小于5%。（常用的低视能辅具的放大效果大约为2× 到10×，或 200%到1000%）。但是，当双眼间存在一点点像大小的差异时，大脑会将其翻译成双目正在感受立体深度的提示。由于立体视觉很敏感，放大效果很小的差异也会对空间感造成很大的问题。这些困难造成的问题在患者适应新眼镜的时候经常会显现出来。双眼间的差异在0.8%到1%之间就是问题会出现的临界范围^[13]。

无论是柱镜度数差异还是柱镜轴差异，双眼散光矫正差异造成的放大效果差异有可能会造成两个像大小的不同以及形状的不同。斜柱镜（柱镜轴接近45或135度）往往会发生最多的问题，患者一般在柱镜度数小于等于0.75D时会反馈有问题。

等式2中的镜片放大率公式无法用来计算有屈光参差的双眼间的放大率差。放大率之所以难计算是因为，当用矫正镜片来观察未矫正的像的大小时，镜片放大率公式会与视网膜像的大小有关。除非两眼中未矫正的视网膜像的大小是一样的，否则镜片放大率公式是无法提供相关像的大小信息的。举个例子，如果右眼的镜片放大率计算出来是5%，而左眼的是2%。我们不能说右眼的像就比左眼的像大3%，因为未矫正的左右眼的像在戴眼镜之前也许本来就是不同的。要计算双眼间视网膜像大小的差需要知道如轴长，屈光度之类的参数^[26]，这些信息往往不易得到。要准确的测量这个差必须要用到光像测定器。

我们不能假设患者对新眼镜的不适都是放大问题造成的。而明显要问的问题是，“患者旧眼镜的度数是多少”以及“患者在过去适应别的眼镜时是否都会有问题？”。古话中提到不要根据患者旧眼镜的数值来改变新眼镜基弯的说法是几乎毫无意义的，因为新的光度放大率差通常要远远大于形状放大率差的改变。在尝试解决一个可能是放大率的问题之前，镜片应先得到全面的度数检查，并按照生产商表格核对基弯。

双眼物像不等

当屈光参差者无法适应两块镜片的放大效果差异时，他就得了临床上较严重的双眼物像不等。因为光像测定仪临床上很少有，双眼物象不等通常会基于临床迹象和症状来诊断和整治，从折射误差的差异来估计放大率差^[27]-[30]。双眼物像不等的矫正需要改变基弯和中心厚度（改变形状系数），让它们不再是正常值，从而改变视网膜像的放大效果。为了这个目的设计的眼镜片称为影像镜片或等像镜片。这种镜片通常很贵，且很难在光学实验室生产。

与其提供影像镜片，从业人员更常做的是通过修改处方来减弱镜片适应的问题，或双眼物像不等。当散光矫正位于斜轴上时，患者经常会反馈像有畸变（如墙或地面有倾斜，地面太近或太远）。通常这些问题可以通过降低散光度数，或柱镜轴转动180度或90度，而被弱化或清除。虽然最后模糊的成像会降低对图像放大效果的敏感度，处方的修改可以被认作是镜片放大效果的修改。另一种常用的通过镜片解决双眼物像不等的方法是部分矫正较大的球面屈光参差，例如由于一只眼睛核性白内障初期造成的屈光参差。这些类型的处方修改需要可靠的临床判断，因为它们牺牲了视敏度，但却在不尝试矫正双眼物像不等的情况下，提供了一种可以接受的方法。

基弯表——一张设计的“蓝图”

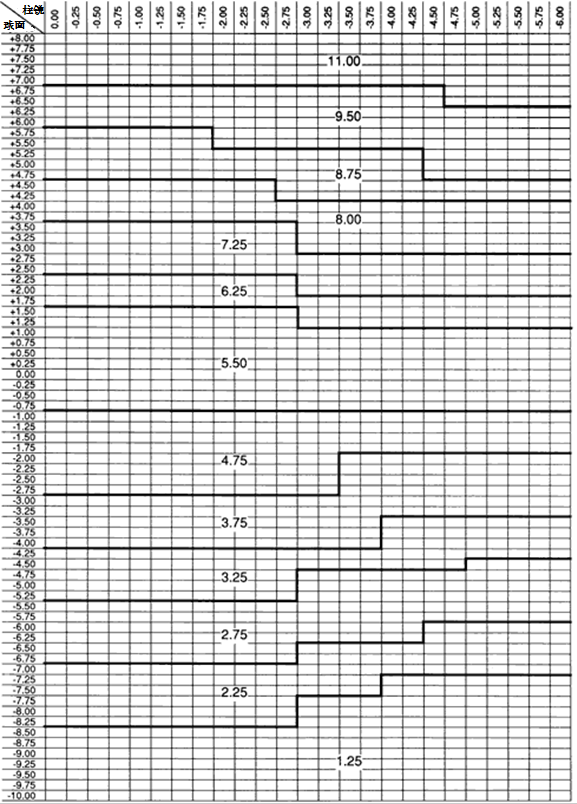
基弯表记录了镜片设计中每个给定度数所对应的基弯。若背面弯度和中心厚度也包括在内的话，则表格应被叫做面表，因为它提供了制造一块成品镜片需要的所有信息。图13为一个镜片系列假设的基弯表。之所以称之为假设是因为基弯和它们之间的界限不是通过计算而来，不代表任何现有的镜片系列。这类表专门在实验室作为指南，用于半成品毛坯的选择，然后进一步做处方铣磨。如果基弯是根据镜框配戴距离而选择的，类似的表还可以在眼镜药房使用。

图13.假设基弯表

在眼镜业，基弯表就是镜片设计的陈述。因为基弯表描述了一个系列中每个镜片的结构，因此某种意义上，它是设计师对于不同处方选择基弯的蓝图和指南。当装配师根据品牌来订购处方上的镜片时，他可以知道镜片的基弯会是多少。当收到镜片时，基弯的选择可以根据表格来核对。

处方上度数在+8.00D到10.00D之间的球镜部分可以通过在横排中找到。柱镜部分，从0.00到-6.00D（标在页面最上方），可以在竖排中找到。每个横排和竖排相交的方框里都代表了可能的球柱镜处方。知道处方和1.53的基弯后，光学实验室可以很容易地决定凹面弯度。某些表在左边还会标有一列厚度。另一些则会用分开的表格。这张表包含了许多设计中需要考虑的方面。在分析假设设计时，需要考虑到以下几个重要的点：

1.  基弯有很多个。虽然基弯数量越多可以得到的光学质量越好，但现有的基弯数量已经足够提供一个较好的质量了。生厂商应在表中添加设计标准和允许范围的信息。

2.  表中不同柱镜值对应的基弯是交错在整张表的。显然，单独一个球面所选的基弯，与同样球面但有-6.00D散光所选的基弯是不同的。但某些镜片系列是没有变化的，它们在表中的水平界限是呈直线的。然而，Z字形的界限是非常少的。一个好的系列，在负值区间内，每个基弯会有8到10个Z字。非球面设计的Z字会出现的少些，甚至在表中的某些区域内完全没有。生产商应提供关于设计性能的信息。

3.  在高正值区域内有一个+1.50-D的基弯间隔。对于如此厚的镜片这一间隔太大了。+7.00-D镜片的厚度大约为6mm，导致一块基弯+9.50-D屈光度+6.75-D的镜片，与一块基弯+11.00-D屈光度+7.00-D的镜片之间的形状放大率差大约为0.6%。在高正值区域内，为了最小化这些很少使用的镜片毛坯的库存，有时会牺牲放大率差，或某种程度上牺牲视野误差。

参考文献

1. Schwartz JT, Ogle KN: The depth of focus of the eye. Arch Ophthalmol 61:578, 1959

2. Campbell FW: The depth of field of the human eye. Optica Acta 4:157, 1957

3. Peters HB: The relationship between refractive error and visual acuity at three age levels. Am J Optom Arch Am Acad Optom 38:194, 1961

4. Sloan LL: Measurement of visual acuity: A critical review. Arch Ophthalmol 45:704, 1951

5. Allen MJ: Vision and Highway Safety, p 56. Philadelphia: Chilton, 1970

6. Davis JK: Prescribing for visibility. Probl Optom 2:131, 1990

7. Richards OW: Vision at levels of night road illumination: XII. Change of acuity and contrast sensitivity with age. Am J Optom Arch Am Acad Optom 43:313, 1966

8. Pitts DG: The effects of aging on selected visual functions: Dark adaptation, visual acuity, stereopsis, and brightness contrast. In Sekuler R, Kline D, Dismukes K (eds): Aging and Human Visual Function, pp 131–159. New York: Alan R Liss, 1982

9. American National Standard for Ophthalmics-Prescription Ophthalmic Lenses-Recommendations. ANSI Z80.1-1995. New York: American National Standards Institute, 1995

10. Owens DA: The resting state of the eyes. Am Scientist 72:378, 1984

11. Tunnacliffe AH, Hirst JG: Optics, pp 178–213. 2nd ed. London: Association of British Dispensing Opticians, 1996

12. Fannin TE, Grosvenor T: Clinical Optics, pp 134–141. 2nd ed. Boston: Butterworth-Heinemann, 1996

13. Atchison DA: The clinical importance of spectacle lens base curves. Clin Exp Optom 69:31, 1986

14. Davis JK: Geometric optics in ophthalmic lens design. Proc Soc Photo-Optical Instrum Engineers 39:65, 1973

15. Prentice CF: A metric system for numbering and measuring prisms. Arch Ophthalmol 19:64–75, 128–135, 1890

16. Bechtold EW, Langsen AL: The effect of pantoscopic tilt on ophthalmic lens performance. Am J Optom Arch Am Acad Optom 42:515, 1965

17. Atchison DA, Tame SA: Sensitivity of off-axis performance of aspheric spectacle lenses to tilt and decentration. Ophthalmic Physiol Opt 13:415, 1993

18. Davis JK: A polycarbonate ophthalmic prescription lens series. Am J Optom Physiol Opt 55:543, 1978

19. Smith WJ: Modern Optical Engineering: The Design of Optical Systems, pp 281–325. 2nd ed. Boston: McGraw-Hill, 1990

20. Atchison DA: Spectacle lens design—development and present state. Aust J Optom 67:97, 1984

21. Davis JK, Fernald HG, Rayner AW: The design of a general purpose single vision lens series. Am J Optom Arch Am Acad Optom 42:203, 1965

22. Davis JK, Fernald HG, Rayner AW: An analysis of ophthalmic lens design. Am J Optom Arch Am Acad Optom 41:400, 1964

23. Davis JK, Fernald HG, Rayner AW: The Tillyer Masterpiece Lens: A Technical Discussion. Southbridge, MA: American Optical, 1964

24. Davis JK, Fernald HG, Rayner AW: Ophthalmic lens series. US Patent 3,434,781, 1969

25. Ogle KN: Researches in Binocular Vision, p 125. New York: Hafner, 1972

26. Rabbetts RB: Bennett and Rabbetts' Clinical Visual Optics, p 236. 3rd ed. Oxford: Butterworth-Heinemann, 1998

27. Linksz A, Bannon RE: Aniseikonia and refractive problems. Int Ophthalmol Clin 5:515, 1965

28. Enoch JM: Management of aniseikonia after intraocular lens implantation or refractive surgery. J Refract Surg 13:79, 1997

29. Polasky M: Aniseikonia Cookbook II. Columbus: Ohio State University College of Optometry, 1990

30. Stephens GL, Polasky M. New options for aniseikonia correction: The use of high index materials. Optom Vis Sci 68:899, 1991